출처
https://www.acmicpc.net/problem/1922

풀이 전략
문제에서 Minimum Spanning Tree 알고리즘을 사용하라고 힌트를 줬기 때문에 Prim 알고리즘이나 Kruskal 알고리즘을 사용하여 풀이를 할 것이다.
Prim보다는 Kruskal이 구현이 약간?은 더 간단할 것 같아서 Kruskal 알고리즘으로 풀었다.
Pseudo Code

풀이

수도 코드에서 보면 알겠지만, Kruskal Algorithm의 특징은 Union-Find를 사용한다는 점과 edge를 weight가 작은 순으로 정렬해서 최솟값을 찾는다는 점이다. 그렇기 때문에 위의 그림과 같은 순서가 나온다.
다만, 5번째의 경우 weight가 8인 edge가 4-6과 5-6 둘 다 가능한데, 문제 힌트에서 4-6이라고 주어져 있어서 4-6을 색칠하긴 했지만 5-6을 해도 아무 문제가 없다.
소스 코드
#include <iostream>
#include <vector>
#include <algorithm>
#define MAX 100001
using namespace std;
int N,M;
int result=0;
int Parent[MAX];
vector<pair<int,pair<int,int>>> Edge;
int Find(int x){
if(Parent[x]==x)
return x;
else
return Parent[x]=Find(Parent[x]);
}
void Union(int x, int y){
x=Find(x);
y=Find(y);
if(x!=y)
Parent[y]=x;
}
bool SameParent(int x, int y){
x=Find(x);
y=Find(y);
if(x==y)
return true;
else
return false;
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin>>N>>M;
for(int i=0;i<M;i++){
int a,b,c; // a: 시작점, b: 도착점, c: weight
cin>>a>>b>>c;
Edge.push_back(make_pair(c,make_pair(a,b)));
}
// weight가 작은 순서대로 정렬
sort(Edge.begin(), Edge.end());
for(int i=1;i<=N;i++){
Parent[i]=i;
}
for(int i=0;i<M;i++){
// a와 b가 같은 부모를 갖지 않는다면
if(!SameParent(Edge[i].second.first, Edge[i].second.second)){
// a와 b를 Union
Union(Edge[i].second.first, Edge[i].second.second);
// weight 값을 더해줌
result+=Edge[i].first;
}
}
cout<<result<<'\n';
return 0;
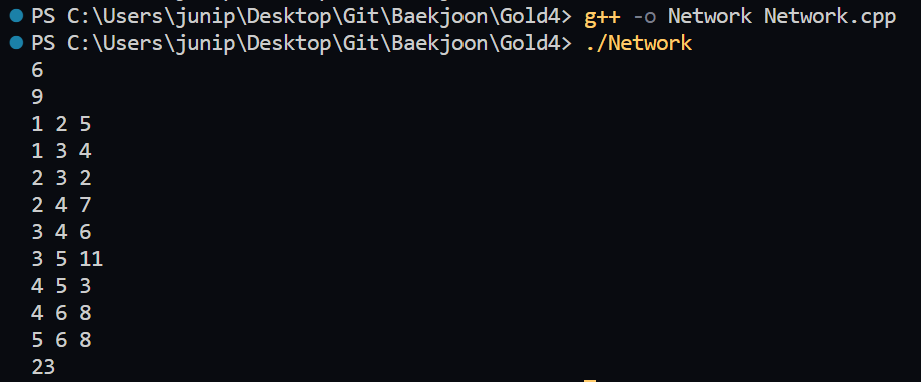
}결과
'Baekjoon' 카테고리의 다른 글
| [Python] 백준 1992 - 쿼드트리 [Silver1] | 2024.09.11 |
|---|---|
| [C++] 백준 24042 - 횡단보도 [Gold1] | 2024.09.10 |
| [C++] 백준 2565 - 전깃줄 [Gold5] | 2024.09.10 |
| [C++] 백준 5095 - Matrix Powers [Gold4] | 2024.09.10 |
| [C++] 백준 1504 - 특정한 최단 경로 [Gold4] | 2024.09.10 |