
출처
https://www.acmicpc.net/problem/1504
풀이 전략
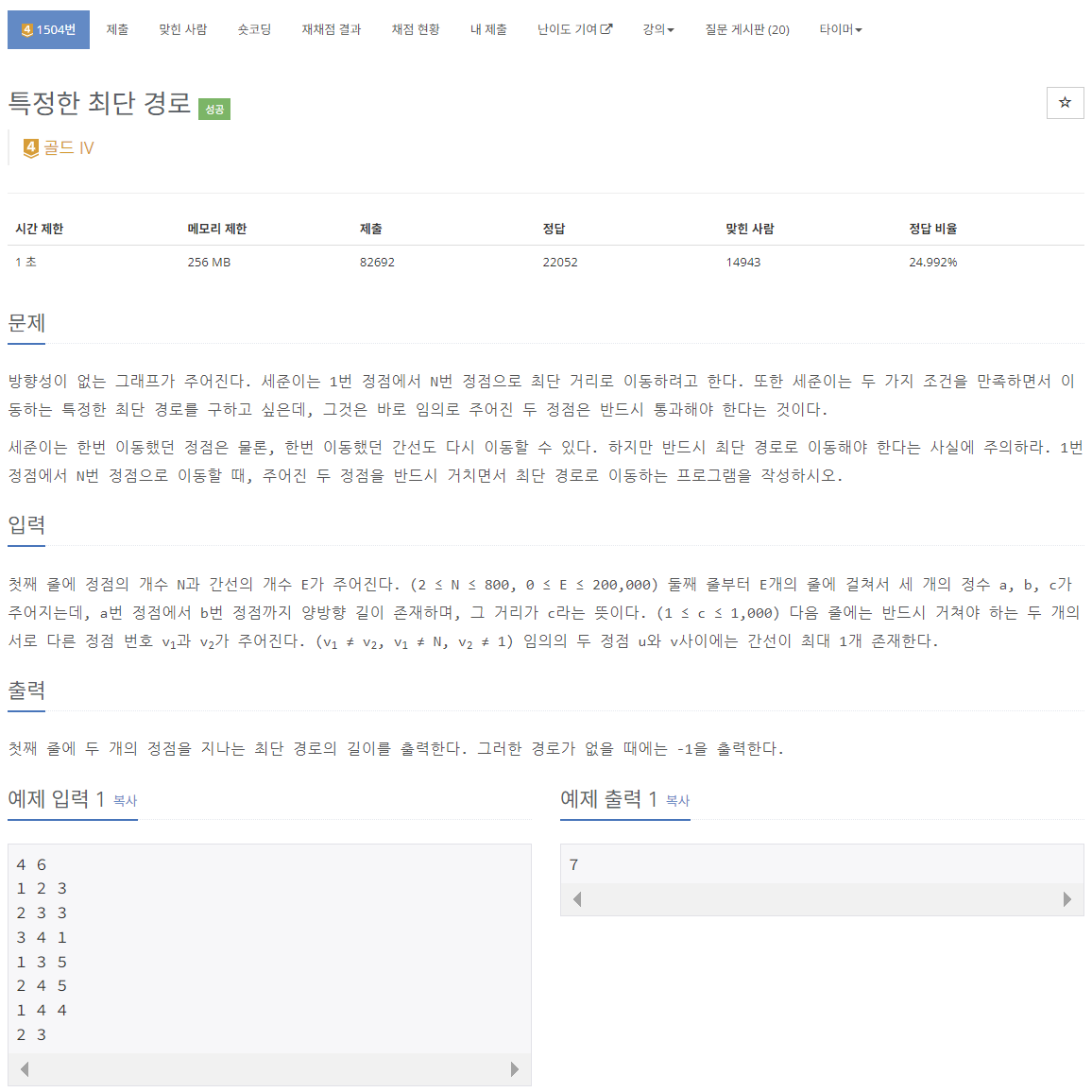
Dijkstra 알고리즘을 이용하여 최단경로를 구할 것이다. 다만, 이 문제의 경우 마지막에 입력 받는 v1과 v2를 무조건적으로 거친 경로 중 최단 경로를 찾는 것이기 때문에 세 가지 경우로 나누어서 구할 것이다.
- from 1번 (시작 정점) to v1
- from v1 to v2
- from v2 to N번 (도착 정점)
세 가지의 경우로 나눈 최단 경로를 모두 더해주면 정답이 구해질 것이라고 생각하고 문제를 접근했다
풀이

문제의 예시를 그림으로 그려보면 위의 그림과 같다. 첫번째 예시를 보면 2-3을 지나는 최단경로를 찾으면 1-2-3-4로 총 합은 7이 된다. 이 경우, 모든 vertex가 연결되어 있기 때문에 인접노드행렬을 그려보면 INF가 없다. 그렇기 때문에 이 예시의 경우 경로가 없을 때 출력이 되는 -1이 출력될 일이 없다.
그래서 임의로 두 번째 예시를 넣어 보았다.
이 경우 만약 4,5를 무조건 지나라고 할 경우 경로의 cost가 INF이기 때문에 -1이 출력될 것 처럼 보이지만 마지막에 4에서 5까지 가는 모든 경로와 INF 둘을 비교해서 최솟값을 출력하라고 코드를 적었기 때문에 return 값이 INF가 되려면 무인도 같은 노드가 있어야 한다.
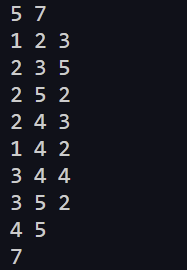
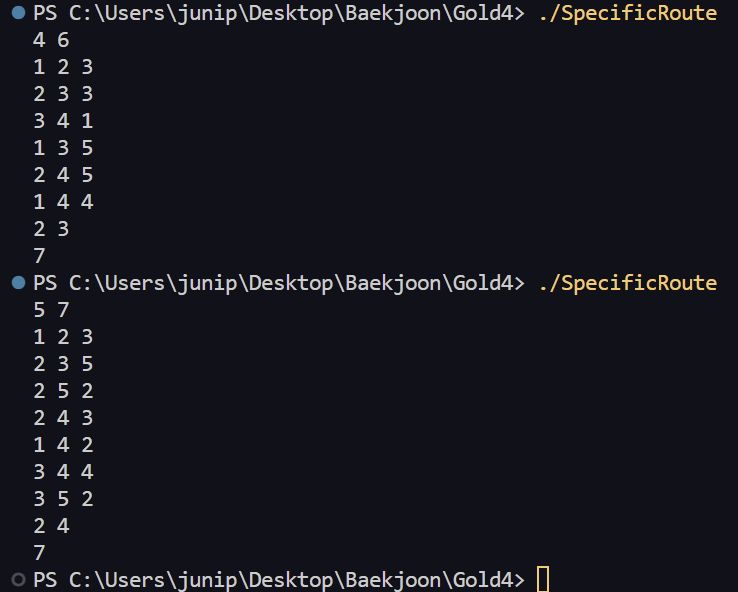
그래서 4 5를 입력했는데 7이 출력된 것을 보고 의아했지만 1-4-2-5 경로를 보면 어쨋든 4에서 5까지 가는 경로이기 때문에 ans1 = 7, ans2 = INF 이 둘을 min 함수로 비교한 결과 7이 return 값으로 나와서 7이 출력된다.
소스 코드
/*
# Question: BJ 1504 (https://www.acmicpc.net/problem/1504)
# Rank: Gold4
# Algorithm: Graph, Dijkstra, Shortest Path
*/
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#define MAX 801
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int INF = 1e9;
int N, E, v1, v2, ans1, ans2;
vector<pii> adj[MAX];
int dist[MAX];
void Input();
int Dijkstra(int start, int end);
int FindShortestPath(int v1, int v2);
void Input(){
cin >> N >> E;
for (int i = 0; i < E; i++){
int a, b, c;
cin >> a >> b >> c;
adj[a].push_back({c, b});
adj[b].push_back({c, a});
}
cin >> v1 >> v2;
}
int Dijkstra(int start, int end){
for(int i=1; i<=N; i++){
dist[i] = INF;
}
priority_queue<pii, vector<pii>, greater<pii>> pq;
pq.push({0, start});
dist[start] = 0;
while(!pq.empty()){
int curDist = pq.top().first;
int cur = pq.top().second;
pq.pop();
if(dist[cur] < curDist)
continue;
for(int i = 0; i < adj[cur].size(); i++){
int nextDist = adj[cur][i].first;
int nextVertex = adj[cur][i].second;
if(dist[nextVertex] > curDist + nextDist){
dist[nextVertex] = curDist + nextDist;
pq.push({dist[nextVertex], nextVertex});
}
}
}
return dist[end];
}
// v1, v2를 거치는 경로 중 최단 경로 찾기
int FindShortestPath(int v1, int v2){
ans1 = INF, ans2 = INF;
if (Dijkstra(1, v1)==INF || Dijkstra(v1, v2)==INF || Dijkstra(v2, N)==INF)
ans1 = INF;
else
ans1 = Dijkstra(1, v1) + Dijkstra(v1, v2) + Dijkstra(v2, N);
// 1-> V2 -> V1 -> N 끊기는 부분 있는지 체크
if (Dijkstra(1, v2)==INF || Dijkstra(v2, v1)==INF || Dijkstra(v1, N)==INF)
ans2 = INF;
else
ans2 = Dijkstra(1, v2) + Dijkstra(v2, v1) + Dijkstra(v1, N);
return min(ans1, ans2);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
Input();
FindShortestPath(v1, v2);
// 정답 출력
if (ans1 == INF && ans2 == INF)
cout << "-1";
else
cout << min(ans1, ans2);
return 0;
}참고로 말하면, Dijkstra 함수에서 처음에 dist 배열을 INF로 초기화 하는 과정을 for문으로 1부터 N까지 하는 것이 아니라 fill(dist, dist+N, INF)로 했더니 계속 6이 출력이 되었다. 그 이유를 생각해보니 dist부터 dist+N까지 하면 for문으로 따지면 for(int i=0; i<N; i++)과 같기 때문에 0번 노드 부터 N-1번째 노드를 INF로 초기화 한 셈이 되어 3번에서 4번으로 가는 경로의 cost 1을 안더하게 되어 6이 출력된 것 같다.
따라서 fill 함수를 쓰려면 dist와 dist+N 각각 1씩 더 더해주면 제대로 출력될 것이다.
결과
참고
https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm
Dijkstra's algorithm - Wikipedia
From Wikipedia, the free encyclopedia Algorithm for finding shortest paths Dijkstra's algorithm ( DYKE-strəz) is an algorithm for finding the shortest paths between nodes in a weighted graph, which may represent, for example, road networks. It was conceiv
en.wikipedia.org
Pseudo code
function Dijkstra(Graph, source):
for each vertex v in Graph.Vertices:
dist[v] ← INFINITY
prev[v] ← UNDEFINED
add v to Q
dist[source] ← 0
while Q is not empty:
u ← vertex in Q with min dist[u]
remove u from Q
for each neighbor v of u still in Q:
alt ← dist[u] + Graph.Edges(u, v)
if alt < dist[v]:
dist[v] ← alt
prev[v] ← u
return dist[], prev[]'Baekjoon' 카테고리의 다른 글
| [C++] 백준 2565 - 전깃줄 [Gold5] (0) | 2024.09.10 |
|---|---|
| [C++] 백준 5095 - Matrix Powers [Gold4] (1) | 2024.09.10 |
| [C++] 백준 2636 - 치즈 [Gold4] (1) | 2024.09.10 |
| [Python] 백준 2583 - 영역 구하기 [Silver1] (0) | 2024.09.10 |
| [C++] 백준 25206 - 너의 평점은 [Silver5] (0) | 2024.09.10 |