
출처
https://www.acmicpc.net/problem/24042

풀이 전략
이 문제의 경우 일반적인 dijkstra 문제와는 살짝 다르다.
신호등이 바뀌는 순서를 고려할 뿐더러 만약 경로에 순서가 늦는 신호등이 있는 경우 신호등의 주기만큼 기다려야 한다.
따라서 일반적인 Dijkstra 알고리즘의 틀에서 cost를 계산하는 부분을 잘 계산해야한다.
풀이

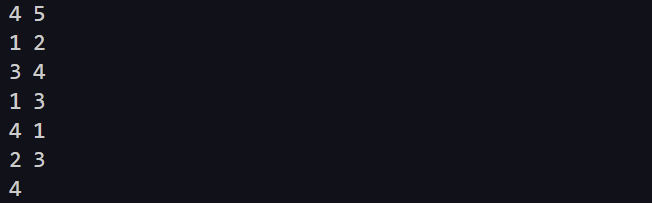
왼쪽에 있는 첫 번째 예제의 경우 1-4 로 가는 최단 경로는 1-4 방향 신호등이 4번째에 바뀌기 때문에 정답은 4인 것을 쉽게 알 수 있다.
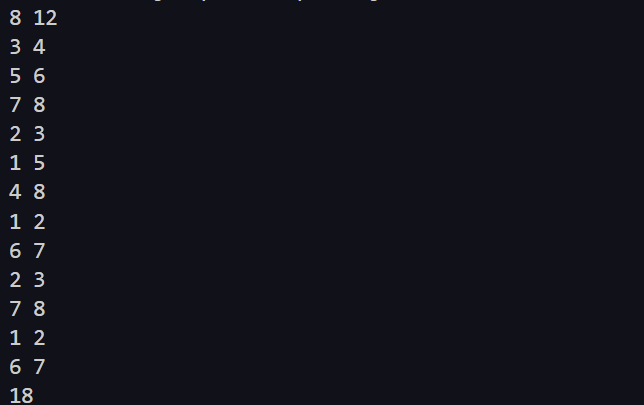
그러나 오른쪽에 있는 두 번째 예제의 경우 1-8로 한번에 가는 경로가 없기 때문에 여러 신호등을 거쳐 가야하므로 고려해야할 부분이 많다.
먼저 정답이 되는 경우의 계산 방식을 보면,
- 1-2 횡단보도가 7번째에 바뀌기 때문에 현재의 cost = 7
- 2-3 횡단보도가 4번째에 바뀌기도 하지만, 7번째보다 뒤에 있는 9번째에도 바뀌기 때문에 더 빨리 바뀌는 9번째 순서로 건너가게 된다. 이 때, 현재의 cost는 7+9=16이 아니라 9번째에 건넜기 때문에 9이다.
- 3-4를 건너는 순서는 제일 첫번째인데, 이전에 건넌 횡단보도가 9번째이기 때문에 주기 12까지 기다린 다음에 건너야 한다.
여기서, 이 관계에 대한 식을 구해야 한다.
기존의 일반적인 경우에 대한 식은 다음 지역으로 건너는 순서 - 현재까지의 cost + 건너는 시간 (1)로 나타낼 수 있다.
건너는 시간은 나중에 일괄적으로 더하기 때문에 건너는 시간을 제외한 코드를 보면 다음과 같다.
nextCost += (i.second - cost) % M;그러나 만약 다음 지역으로 건너는 횡단보도가 1개인데 그 순서가 방금 건넌 횡단보도보다 빠를 경우 모든 횡단보도가 켜졌다 꺼질 때까지 기다렸다가 다시 그 횡단보도의 차례가 되었을 때 건너야 한다.
그러므로 다음 지역으로 건너는 순서 - 현재까지의 cost가 음수가 나올 것이고 그 값이 주기 M을 더해준 뒤, 연산 결과를 다시 M으로 나눈 나머지를 반환하면 그 값이 기다린 시간이 되게 된다.
이를 코드로 나타내면 다음과 같다.
nextCost += ((i.second - cost) % M + M) % M;기존의 Dijkstra algorithm의 틀에서 cost를 구하는 부분만 위의 두 코드로 바꿔주면 된다.
소스 코드

결과
'Baekjoon' 카테고리의 다른 글
| [C++] 백준 7869 - 두 원 [Gold2] (1) | 2024.09.11 |
|---|---|
| [Python] 백준 1992 - 쿼드트리 [Silver1] (1) | 2024.09.11 |
| [C++] 백준 1922 - 네트워크 연결 [Gold4] (0) | 2024.09.10 |
| [C++] 백준 2565 - 전깃줄 [Gold5] (0) | 2024.09.10 |
| [C++] 백준 5095 - Matrix Powers [Gold4] (1) | 2024.09.10 |